There are four varieties of Airy functions: 
, 
, 
, and 
. Of these, 
and 
are by far the most common, with 
and 
being encountered much less frequently. Airy functions
commonly appear in physics, especially in optics, quantum mechanics, electromagnetics,
and radiative transfer.
and 
are entire functions.
A generalization of the Airy function was constructed by Hardy.
The Airy function 
and 
functions are plotted above along the real axis.
The 
and 
functions are defined as the two linearly independent
solutions to
 |
(1)
|
(Abramowitz and Stegun 1972, pp. 446-447; illustrated above), written in the form
 |
(2)
|
where
 |  |  |
(3)
|
 |  |  |
(4)
|
where 
is a confluent hypergeometric
limit function. These functions are implemented in the Wolfram
Language as AiryAi[z]
and AiryBi[z].
Their derivatives are implemented as AiryAiPrime[z]
and AiryBiPrime[z].
For the special case 
,
the functions can be written as
 |  | ![1/3sqrt(x)[I_(-1/3)(2/3x^(3/2))-I_(1/3)(2/3x^(3/2))]](/images/equations/AiryFunctions/Inline25.svg) |
(5)
|
 |  |  |
(6)
|
 |  | ![sqrt(x/3)[I_(-1/3)(2/3x^(3/2))+I_(1/3)(2/3x^(3/2))],](/images/equations/AiryFunctions/Inline31.svg) |
(7)
|
where 
is a modified Bessel function
of the first kind and 
is a modified
Bessel function of the second kind.
 |
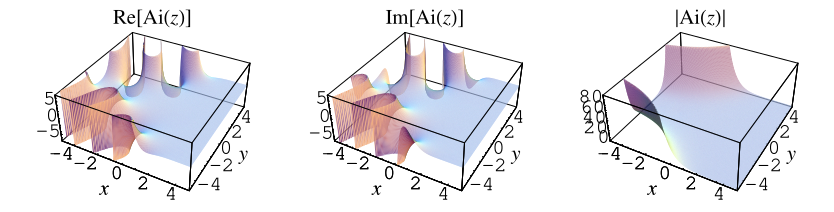
Plots of 
in the complex plane are illustrated above.
 |
Similarly, plots of 
appear above.
The Airy 
function is given by the integral
 |
(8)
|
and the series
 |  | ![1/(3^(2/3)pi)sum_(n=0)^(infty)(Gamma(1/3(n+1)))/(n!)(3^(1/3)z)^nsin[(2(n+1)pi)/3]](/images/equations/AiryFunctions/Inline39.svg) |
(9)
|
 |  | ![1/(3^(1/6)pi)sum_(n=0)^(infty)(Gamma(1/3(n+1)))/(n!)(3^(1/3)z)^n|sin[(2(n+1)pi)/3]|](/images/equations/AiryFunctions/Inline42.svg) |
(10)
|
(Banderier et al. 2000).
For 
,
 |  |  |
(11)
|
 |  |  |
(12)
|
where 
is the gamma function. Similarly,
 |  |  |
(13)
|
 |  |  |
(14)
|
The asymptotic series of 
has a different form in different quadrants
of the complex plane, a fact known as the stokes
phenomenon.
Functions related to the Airy functions have been defined as
 |  |  |
(15)
|
 |  | ![1/3Bi(z)+int_0^z[Ai(z)Bi(t)-Ai(t)Bi(z)]dt](/images/equations/AiryFunctions/Inline63.svg) |
(16)
|
 |  |  |
(17)
|
 |  |  |
(18)
|
 |  | ![2/3Bi(z)+int_0^z[Ai(t)Bi(z)-Ai(z)Bi(t)]dt](/images/equations/AiryFunctions/Inline72.svg) |
(19)
|
 |  |  |
(20)
|
where 
is a generalized hypergeometric
function.
Watson (1966, pp. 188-190) gives a slightly more general definition of the Airy function as the solution to the Airy differential equation
 |
(21)
|
which is finite at the origin, where 
denotes the derivative 
, 
, and either sign is permitted.
Call these solutions 
,
then
 |
(22)
|
 |  | ![1/3pisqrt(z/3)[J_(-1/3)((2z^(3/2))/(3^(3/2)))+J_(1/3)((2z^(3/2))/(3^(3/2)))]](/images/equations/AiryFunctions/Inline83.svg) |
(23)
|
 |  | ![1/3pisqrt(z/3)[I_(-1/3)((2z^(3/2))/(3^(3/2)))-I_(1/3)((2z^(3/2))/(3^(3/2)))],](/images/equations/AiryFunctions/Inline86.svg) |
(24)
|
where 
is a Bessel function of the first kind.
Using the identity
 |
(25)
|
where 
is a modified Bessel function
of the second kind, the second case can be re-expressed
 |  |  |
(26)
|
 |  |  |
(27)
|
 |  |  |
(28)
|
) and Bi(
)." Ch. 56 in