J. Tupper concocted the amazing formula
where  is the floor function and
is the floor function and  is the mod function, which,
when graphed over
is the mod function, which,
when graphed over  and
and  with
with
gives the self-referential "plot" illustrated above.
Tupper's formula can be generalized to other desired outcomes. For example, L. Garron (pers. comm.) has constructed generalizations for  to 29.
to 29.
See also
Self-Recursion
Explore with Wolfram|Alpha
References
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental
Mathematics in Action. Wellesley, MA: A K Peters, p. 289, 2007."Self-Answering
Problems." Math. Horizons 13, No. 4, 19, Apr. 2005.Wagon,
S. Problem 14 in http://stanwagon.com/wagon/Misc/bestpuzzles.html.Referenced
on Wolfram|Alpha
Tupper's Self-Referential
Formula
Cite this as:
Weisstein, Eric W. "Tupper's Self-Referential Formula." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/TuppersSelf-ReferentialFormula.html
Subject classifications
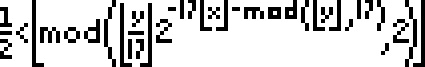
is the floor function and
is the mod function, which,
when graphed over
and
with

to 29.