Synergetics coordinates are a set of triangular coordinates in their plane (or their generalization to tetrahedral coordinates in space, or the analogs in higher dimensions).
In the plane, coordinates are measured along three axes
,
, and
, with the
-axis oriented downward and the
and
axes oriented at
angles to each other as illustrated above (left
figure). Interpreting
,
, and
as points on the sides of an equilateral
triangle obtained by parallel-displacing from the origin three pairs of lines
oriented at
angles with respect to one another, the coordinates
can be interpreted as specifying a given equilateral
triangle (right figure).
A nice property of these coordinates is that the vertices of the triangle obtained by parallel-displacing by are given by
,
, and
(see above figure), so that the sums of the coordinates
of the vertices are always zero. This property also holds when the coordinates are
generalized to three and higher dimensions.
The synergetics coordinates also have the property that the edge lengths of the equilateral triangle described by is precisely
, which again generalizes to higher dimensions.
Synergetics coordinate provide a convenient way to construct regular circle and sphere packings. For example, the ring of circles illustrated above at left can be generated
by picking all sets of integer synergetics coordinates that sum to zero and such that the sum of the absolute
values of the three coordinates divided by two equals one (Nelson). Similarly, the
second ring of circles can be obtained from all sets of integer coordinates that
sum to zero and such that the sum of the absolute values of the three coordinates
divided by two equals one. The zeroth, first, and second rings are illustrated above
at right.
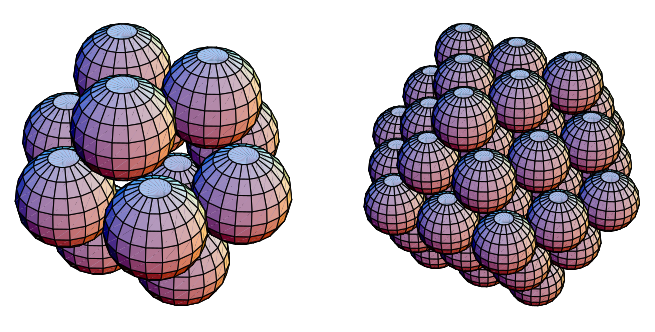
Similar properties hold in three dimensions, where appropriate sets of synergetics coordinates
give successive shells in a regular sphere packing (Nelson), illustrated above.