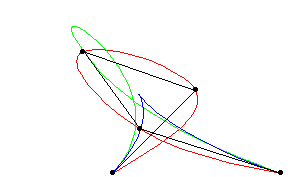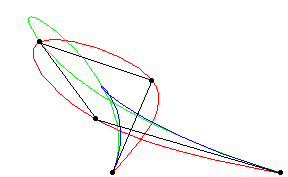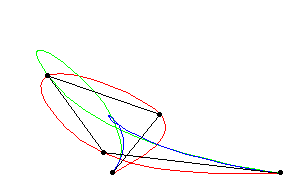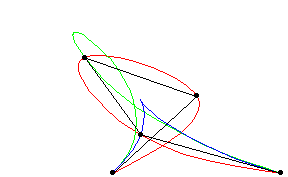
A piecewise polynomial function that can have a locally very simple form, yet at the same time be globally flexible and smooth. Splines are very useful for modeling arbitrary functions, and are used extensively in computer graphics.
Cubic splines are implemented in the Wolfram Language as BSplineCurve pts ,
SplineDegree -> 3 ] (red), Bézier curves
as BezierCurve pts ]
(blue), and B-splines as BSplineCurve pts ].
See also B-Spline ,
Bézier Curve ,
Cubic Spline ,
NURBS
Curve ,
Thin Plate Spline
Explore with Wolfram|Alpha
References Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. An
Introduction to Splines for Use in Computer Graphics and Geometric Modelling. de Boor, C. A
Practical Guide to Splines. Dierckx,
P. Curve
and Surface Fitting with Splines. Micula, G. and Micula, S. Handbook
of Splines. Press, W. H.;
Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Interpolation
and Extrapolation." Ch. 3 in Numerical
Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Späth, H. One
Dimensional Spline Interpolation Algorithms. Weisstein,
E. W. "Books about Splines." http://www.ericweisstein.com/encyclopedias/books/Splines.html . Referenced
on Wolfram|Alpha Spline
Cite this as:
Weisstein, Eric W. "Spline." From MathWorld https://mathworld.wolfram.com/Spline.html
Subject classifications