The spider and fly considers a rectangular room (a cuboid) with dimensions
in which a spider is located in the middle of one
wall one foot away from the ceiling. A fly is
in the middle of the opposite wall one foot away from the floor. If the fly remains
stationary, what is the shortest total distance (i.e., the geodesic)
the spider must crawl along the walls, ceiling, and floor in order to capture the
fly?
The answer, ,
can be obtained by "flattening" the walls as illustrated above. Note that
his distance is shorter than the
the spider would have to travel if first crawling along
the wall to the floor, then across the floor, then up one foot to get to the fly.
The puzzle was originally posed in an English newspaper by Dudeney in 1903 (Gardner
1958).
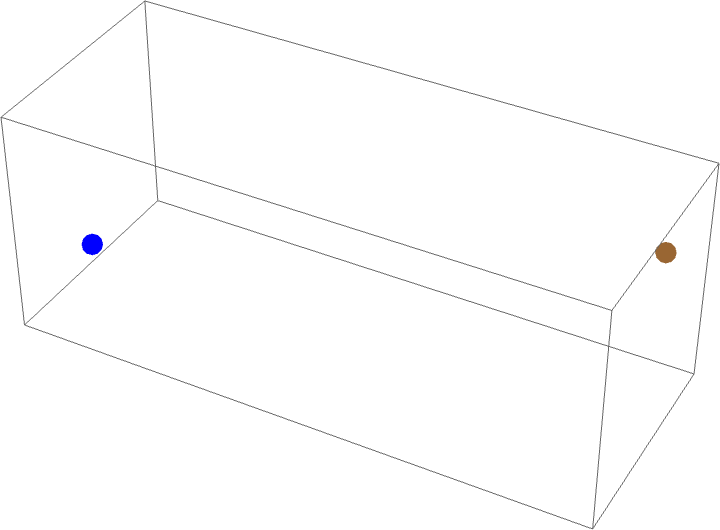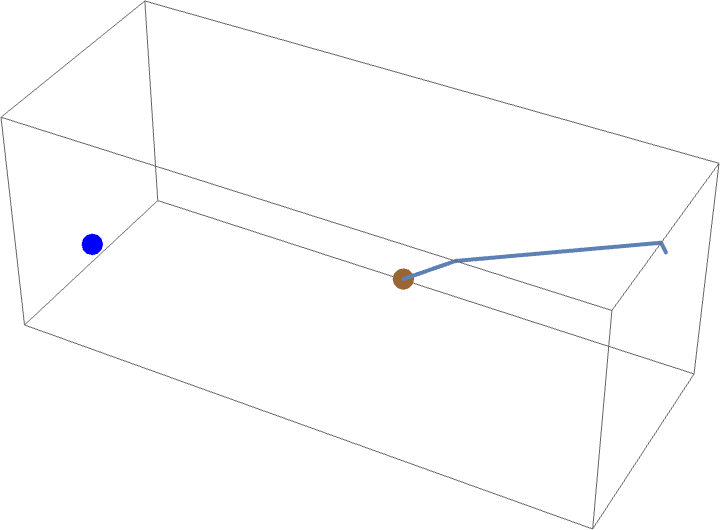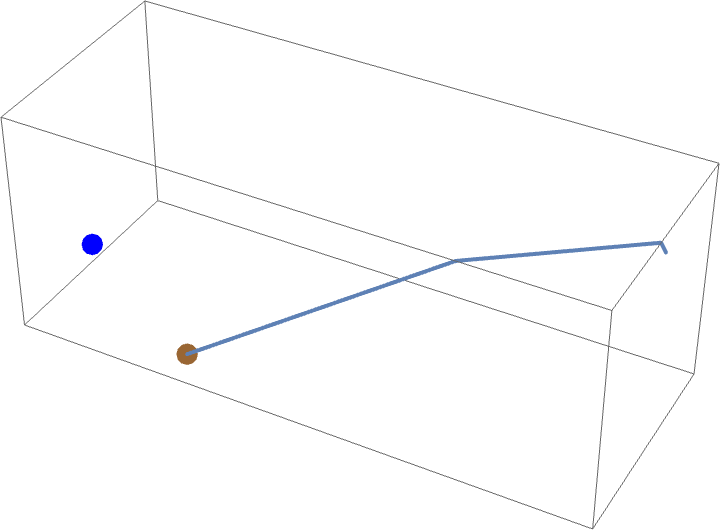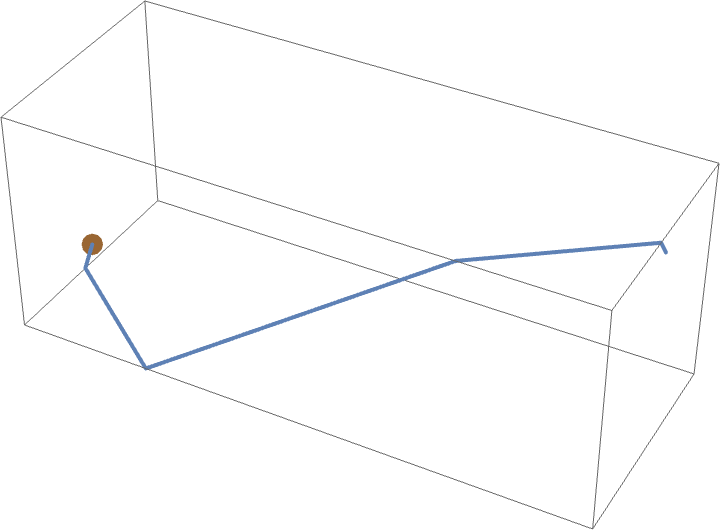
A twist to the problem can be obtained by a spider that suspends himself from strand of cobweb and thus takes a shortcut by not being forced to remain glued to a surface
of the room. If the spider attaches a strand of cobweb to the wall at his starting
position and lowers himself down to the floor (thus not crawling a single inch),
he can then cross the length of the room by foot () and ascend a single foot, thus reaching his prey after
a total crawl of
(although the total distance traveled is of course
).
If the spider is not proficient with fastening strands to vertical walls, he can still get the fly crawling only . In particular, he can climb to the ceiling (
), then traverse the length of the ceiling (
) and lowering himself
(requiring no crawling), thus catching the fly.