A spectral sequence is a tool of homological algebra that has many applications in algebra, algebraic geometry, and algebraic topology. Roughly speaking, a spectral sequence is a system for keeping track of collections of exact sequences that have maps between them.
There are many definitions of spectral sequences and many slight variations that are useful for certain purposes. The most common type is a "first quadrant cohomological
spectral sequence," which is a collection of Abelian
groups
where
,
, and
are integers, with
and
nonnegative and
for some positive integer
, usually 2. The groups
come equipped with maps
|
(1)
|
such that
|
(2)
|
There is the further restriction that
|
(3)
|
The maps
are called boundary maps.
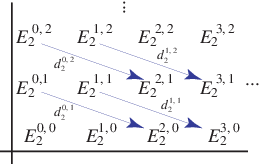
A spectral sequence may be visualized as a sequence of grids, one for each value of .
The
s
and
s
denote positions on the grid, where
is the
-coordinate and
is the
-coordinate. The diagram above shows this for
.
The entire collection of groups together with their boundary maps is referred to as
the
-term.
The groups
are completely determined by the
-term
For any given value of and
, the group
eventually stabilizes, because there are only a finite
number of nonzero boundary maps that either start or end at this position. This stable
value is referred to a
. Stable values allow the convergence of a spectral
sequence to be defined. In particular, the spectral sequence
converges to groups
, written
|
(4)
|
if there is a filtration
|
(5)
|
such that the successive quotients are equal to the terms, i.e.,
|
(6)
|
The Serre spectral sequence is used to compute the cohomology groups of the spaces in a fibration. Suppose
|
(7)
|
is a fibration (for example, the Hopf map ). Then there is a spectral sequence with
-term
|
(8)
|
The sequence converges to . (Here, the
denotes ordinary cohomology and is unrelated to the
's above.) This allows one to compute
the cohomology of one of three spaces
,
, and
from the cohomology of the
other two.
There are other examples of spectral sequences. The Leray-Serre spectral sequence is used to compute the hypercohomology of complexes of sheaves. The Grothendieck spectral sequence is used to compute the derived functors of the composition of two functors from the derived functors of the two original functors. The Leray-Serre spectral sequence is a special case of the Grothendieck spectral sequence. Finally, the Adams spectral sequence is used to compute the higher homotopy groups of spheres.