In general, a triakis octahedron is a non-regular icositetrahedron that can be constructed as a positive augmentation of regular octahedron. Such a solid is also known as a trisoctahedron, especially to mineralogists (Correns 1949, p. 41; Berry and Mason 1959, p. 127). While the resulting icositetrahedron is not regular, its faces are all identical.
The small triakis octahedron, called simply the triakis octahedron by Holden (1971, p. 55), is the 24-faced dual polyhedron of
the truncated cube and is Wenninger dual . The addition of the word "small" is necessary
to distinguish it from the great triakis octahedron,
which is the dual of the stellated truncated
hexahedron. It is illustrated above together with a wireframe version and a net that can be used for its construction.
The small triakis octahedron can be constructed by augmentation of a unit edge-length octahedron by a pyramid with
height .
A small triakis octahedron appears in the middle right as one of the polyhedral "stars" in M. C. Escher's 1948 wood engraving "Stars" (Forty 2003, Plate 43).
It is implemented in the Wolfram Language as PolyhedronData["SmallTriakisOctahedron"].
The small triakis octahedron is the convex hull of the equilateral augmented cube.
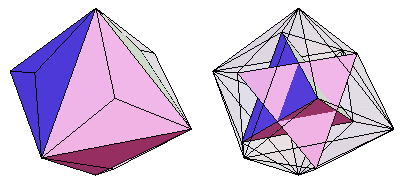
An octahedron and stella octangula can be inscribed on the vertices of the small triakis octahedron (E. Weisstein, Dec. 25, 2009).
The dual polyhedron of the small triakis octahedron is the truncated cube, both of which illustrated above together with their common midsphere. For a truncated cube of unit side length the dual has edges of lengths
|
(1)
| |||
|
(2)
|
Normalizing so that , the resulting small triakis octahedron has surface
area and volume
|
(3)
| |||
|
(4)
|
