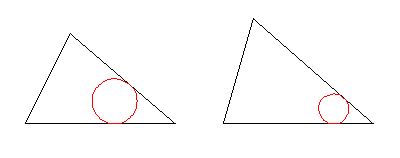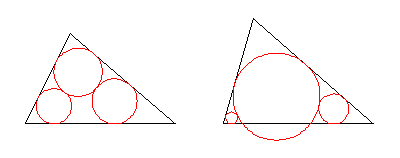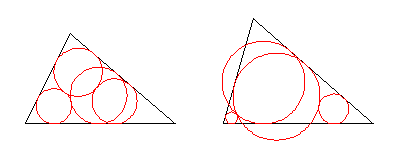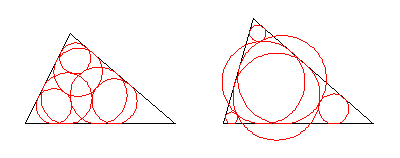
Starting with a triangle, draw a circle touching two sides. Then draw a circle tangent to this circle and two other sides. Continue in the same direction. The result is a chain of circles in which the sixth circle is tangent to the first.
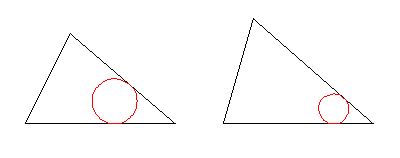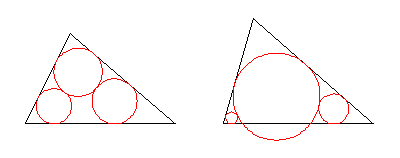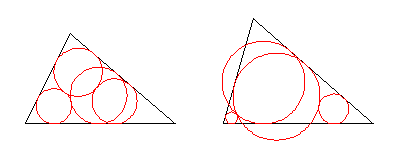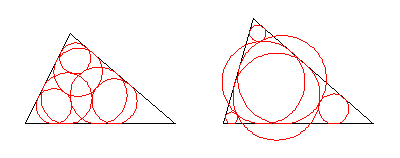
Starting with a triangle, draw a circle touching two sides. Then draw a circle tangent to this circle and two other sides. Continue in the same direction. The result is a chain of circles in which the sixth circle is tangent to the first.
Weisstein, Eric W. "Six Circles Theorem." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/SixCirclesTheorem.html