Semicircle

Half a circle. The area of a semicircle of radius is given by

			(1)
			(2)
			(3)

The weighted mean of is

			(4)
			(5)

The semicircle is the cross section of a hemisphere for any plane through the z-axis.

The perimeter of the curved boundary is given by

(6)

With , this gives

(7)

This property is sometimes, especially in the older literature, referred to as the semicircumference.

The perimeter of the semicircular lamina is then the sum of its semicircumference and diameter:

					(8)
					(9)
					(10)

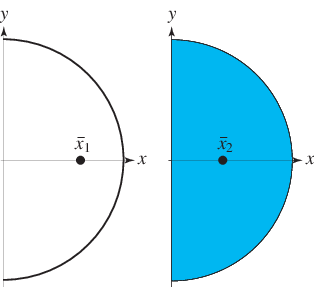
The weighted value of of the semicircular curve is given by

			(11)
			(12)
			(13)

so the geometric centroid is

(14)

The geometric centroid of the semicircular lamina is given by

(15)

(Kern and Bland 1948, p. 113).