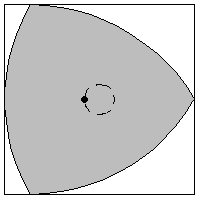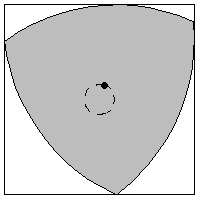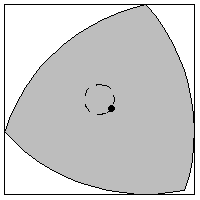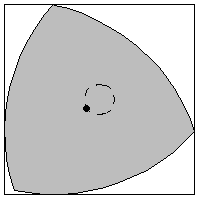
A rotor is a convex figure that can be rotated inside a polygon (or polyhedron) while always touching every side (or
face). The least area rotor in a square
is the Reuleaux triangle. The least area
rotor in an equilateral triangle is a lens with two  arcs of circles
and radius equal to the triangle altitude.
arcs of circles
and radius equal to the triangle altitude.
There exist nonspherical rotors for the tetrahedron, octahedron, and cube, but
not for the dodecahedron and icosahedron.
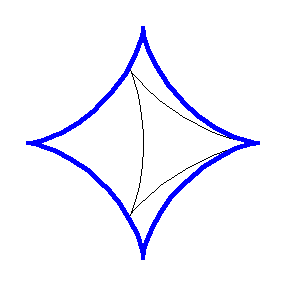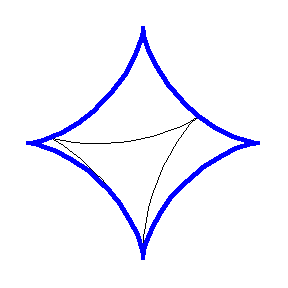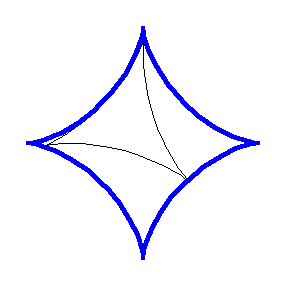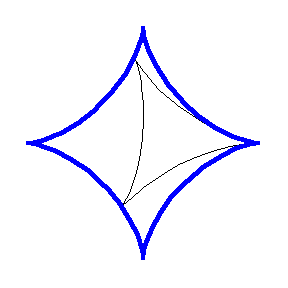
Rotors can also be considered that are not necessarily convex. For example, the animation above illustrates a deltoid rotor inside an astroid
stator.
See also
Delta Curve,
Lens,
Reuleaux Polygon,
Reuleaux
Triangle,
Roulette,
Trip-Let
Explore with Wolfram|Alpha
References
Gardner, M. The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago
University Press, p. 219, 1991.Goldberg, M. "Circular-Arc
Rotors in Regular Polygons." Amer. Math. Monthly 55, 392-402,
1948.Goldberg, M. "Two-Lobed Rotors with Three-Lobed Stators."
J. Mechanisms 3, 55-60, 1968.Steinhaus, H. Mathematical
Snapshots, 3rd ed. New York: Dover, pp. 151-152, 1999.Wells,
D. The
Penguin Dictionary of Curious and Interesting Geometry. London: Penguin,
pp. 221-222, 1991.Referenced on Wolfram|Alpha
Rotor
Cite this as:
Weisstein, Eric W. "Rotor." From MathWorld--A
Wolfram Web Resource. https://mathworld.wolfram.com/Rotor.html
Subject classifications
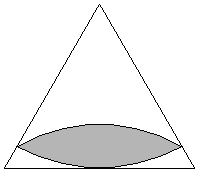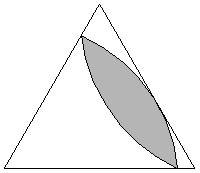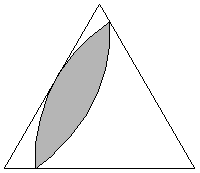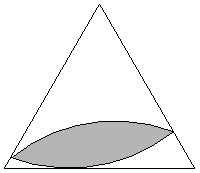
arcs of circles
and radius equal to the triangle altitude.