A square which can be dissected into a number of smaller squares with no two equal is called a perfect square dissection (or a squared square). Square dissections in which the squares need not be different sizes are called Mrs. Perkins's quilts. If no subset of the squares forms a rectangle, then the perfect square is called "simple."
Perfect square dissections correspond to square numbers which are the sum of square numbers. The simplest place to look for such a square might therefore be thought to be square pyramidal numbers. However, there are only two such numbers: 1 and 4900, and even though
 |
it turns out not to be possible to arrange the 24 squares to form a square.

Moron (1925) constructed a perfect rectangle
composed of nine squares of different sizes (Descartes 1971), but Lusin claimed that
perfect squares were impossible to construct. This assertion was proved erroneous
when a 55-square perfect square was published by R. Sprague
in 1939 (Wells 1991). Reichert and Toepkin (1940) proved that a rectangle
cannot be dissected into fewer than nine different squares
(Steinhaus 1999, p. 297).

A 24-square perfect square was subsequently found by Willcocks (Willcocks 1948, 1951; Steinhaus 1999, pp. 8-9).
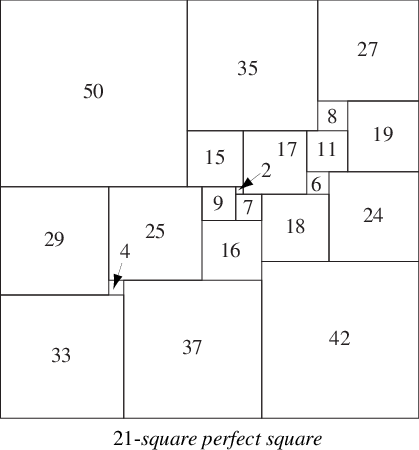
There is a unique simple perfect square of order 21 (the lowest possible order), discovered in 1978 by A. J. W. Duijvestijn (Bouwkamp and Duijvestijn 1992). It is composed of 21 squares with total side length 112, and is illustrated above.
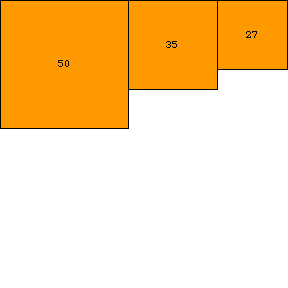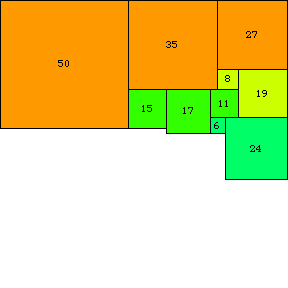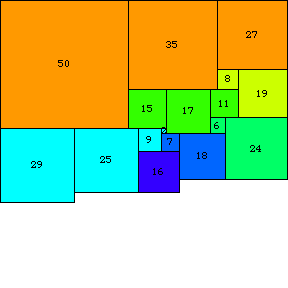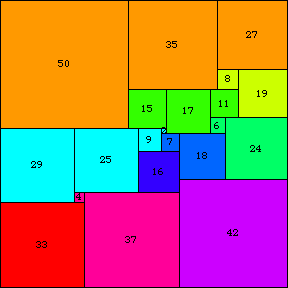
There is a simple notation (sometimes called Bouwkamp code) that can be used to describe perfect squares. In this notation, brackets are used to group adjacent squares with flush tops, and then the groups are sequentially placed in the highest (and leftmost) possible slots. For example, the 21-square illustrated above is denoted [50, 35, 27], [8, 19], [15, 17, 11], [6, 24], [29, 25, 9, 2], [7, 18], [16], [42], [4, 37], [33].
A compound 26-perfect square having side length 608 was discovered in 1940 (Brooks et al. 1940; Kraitchik 1942, p. 198). Beiler (1966) illustrates a compound 28-square and a simple 38-square. Gardner (1961, pp. 203 and 206) illustrates compound 39- and 24-squares.
The number of simple perfect squares of order for
are 1, 8, 12, 26, 160, 441, 1152, ... (OEIS A006983).
Duijvestijn's Table I gives a list of the 441 simple perfect squares of order 26,
the smallest with side length 212 and the largest with side length 825. Skinner (1993)
gives the smallest possible side length (and smallest order for each) as 110 (22),
112 (21), 120 (24), 139 (22), 140 (23), ... for simple perfect squared squares, and
175 (24), 235 (25), 288 (26), 324 (27), 325 (27), ... for compound perfect squared
squares.
There are actually three simple perfect squares having side length 110. They are [60, 50], [23, 27], [24, 22, 14], [7, 16], [8, 6], [12, 15], [13], [2, 28], [26], [4, 21, 3], [18], [17] (order 22; discovered by A. J. W. Duijvestijn); [60, 50], [27, 23], [24, 22, 14], [4, 19], [8, 6], [3, 12, 16], [9], [2, 28], [26], [21], [1, 18], [17] (order 22; discovered by T. H. Willcocks); and [44, 29, 37], [21, 8], [13, 32], [28, 16], [15, 19], [12,4], [3, 1], [2, 14], [5], [10, 41], [38, 7], [31] (order 23; discovered by A. J. W. Duijvestijn).
D. Sleator has developed an efficient algorithm for finding non-simple perfect squares using what he calls rectangle and "ell" grow sequences. This algorithm finds a slew of compound perfect squares of orders 24-32.