The ophiuride is a cubic curve (left figure) given by the implicit equation
 |
(1)
|
where  , or by the polar equation
, or by the polar equation
 |
(2)
|
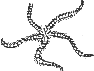
for  . The curve is named
base on its resemblance to a particular species of star-fish (right figure). Taking
. The curve is named
base on its resemblance to a particular species of star-fish (right figure). Taking
 yields a cissoid
of Diocles.
yields a cissoid
of Diocles.
Its curvature is
![kappa(t)=(2{a^2-3b^2+bsec^2t[3b-asectsin(3t)]})/({a^2-3b^2+b^2[2+cos(2t)]sec^4t-4abtant}^(3/2)).](/images/equations/Ophiuride/NumberedEquation3.svg) |
(3)
|
See also
Cissoid of Diocles
This entry contributed by Margherita
Barile
Explore with Wolfram|Alpha
References
Shikin, E. V. Handbook and Atlas of Curves. Boca Raton, FL: CRC Press, pp. 266-267, 1995.Referenced
on Wolfram|Alpha
Ophiuride
Cite this as:
Barile, Margherita. "Ophiuride." From MathWorld--A Wolfram Web Resource, created by Eric
W. Weisstein. https://mathworld.wolfram.com/Ophiuride.html
Subject classifications
, or by the polar equation
. The curve is named
base on its resemblance to a particular species of star-fish (right figure). Taking
yields a cissoid
of Diocles.
![kappa(t)=(2{a^2-3b^2+bsec^2t[3b-asectsin(3t)]})/({a^2-3b^2+b^2[2+cos(2t)]sec^4t-4abtant}^(3/2)).](/images/equations/Ophiuride/NumberedEquation3.svg)