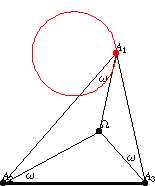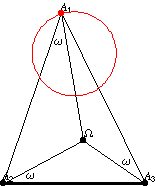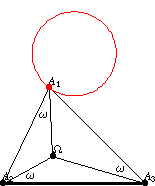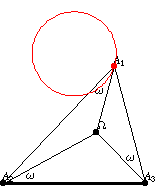
The Neuberg -circle
is the locus of the polygon
vertex
of a triangle on a given base
and with a given Brocard
angle
.
From the center
,
the base
subtends the angle
. The same procedure can be repeated for the other two
sides of a triangle resulting in a total of three Neuberg
circles. Similarly, three reflected Neuberg circles with centers
,
, and
can be obtained from the main circles by reflection in
their respective sides of the triangle.
The equation of the -circle
can be found by taking the base as (0, 0), (
, 0) and solving
|
(1)
| |||
|
(2)
|
while eliminating
and
using
|
(3)
|
where
is the area of the triangle
. Solving for
gives
|
(4)
|
and squaring and completing the square results in
|
(5)
|
Therefore, the Neuberg circle on this edge has center
|
(6)
|
and radius
|
(7)
|
The centers of the Neuberg circles are called Neuberg centers, and the triangles determined by the Neuberg centers are called the first and second Neuberg triangles.
No Kimberling centers lie on any of the Neuberg circles or Neuberg reflected circles.
The circle parameters of the Neuberg circles are given by
|
(8)
| |||
|
(9)
| |||
|
(10)
|
The first Neuberg triangle (left figure) and reflected first
Neuberg triangle
(right figure) are illustrated above.
On one side of a given line taken as a base, it is possible to construct six triangles directly or inversely similar to a given scalene triangle, and the vertices of these triangles lie on their common Neuberg circles (Johnson 1929, p. 289).