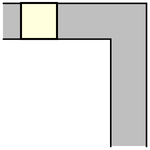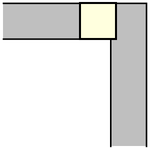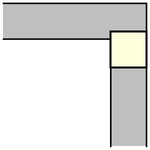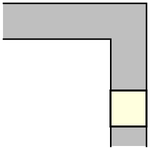
Moser (1966) asked for the plane figure ("sofa") of largest area that can be moved around a right-angled corner in a two-dimensional
hallway of unit width. A unit square with
can be trivially moved "around" the corner
simply by pushing it along the hall until it hits the far wall, then pulling it along
the perpendicular hallway, as illustrated above (Rommik 2016).
While the unit square can be moved "around" the corner without rotation, moving larger shapes is possible when they are allowed
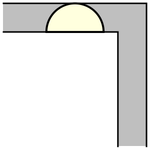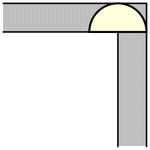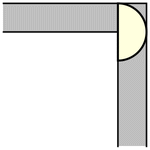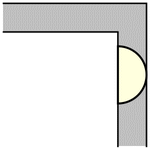
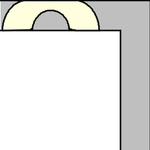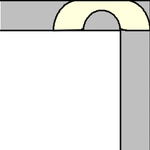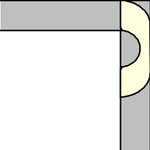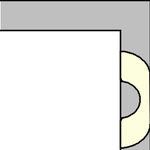
to rotate. The simplest such shape to consider is the half-unit disk (filled semicircle)
with ,
which can be slid around the corner as shown above (Rommik 2016).
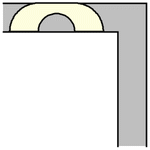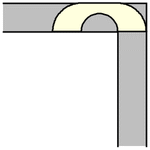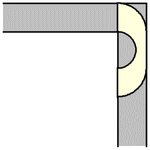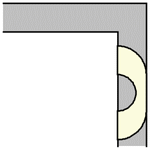
Hammersley (Croft et al. 1994, Rommik) increased the area further by cutting the half-disk into two quarter-disks, separating them horizontally by a distance
while filling in the gap between them. Additionally, he removed a smaller half-disk
of radius
from the bottom, yielding a shape that may be termed the Hammersley
sofa. Its area is maximized when
, giving an area
(OEIS A086118; Croft et al. 1994, Rommik). As it turns out, the Hammersley sofa can move around the corner for any value , including the radius
giving a maximum area. The process
is illustrated above for the maximal Hammersley sofa (Romik 2016).
Gerver (1992) found a sofa with area 2.219531...(OEIS A128463; a number that may be called the moving sofa constant), slightly larger than the 2.207416... (OEIS A086118) area for Hammersley's optimal sofa. This sofa can be moved around a corner, and Gerver (1992) provided arguments indicating that it is either optimal or close to it. The boundary of Gerver's sofa is a complicated shape composed of 3 straight line segments and 15 curved pieces, each of which is described by an analytic expression. An animation of the Gerver sofa rounding the turn is shown above (Romik 2016).
Assuming convex trajectories and envelopes, Deng (2024) used the calculus of variations to formulate an integral functional on a set of parametric equations for curves that determined the sofa shape by solving the Euler-Lagrange differential equation. Using numerical methods, this gave a shape with area 2.2195316, consistent with Gerver's sofa. Baek (2024) showed that Gerver's construction attains the maximum area 2.2195...using a proof does not require computer assistance except for numerical computations that can be done on a scientific calculator.