The function
|
(1)
|
defined on the unit disk . For
, the Köbe function is a schlicht
function
 |
(2)
|
with
for all
(Krantz 1999, p. 149). For
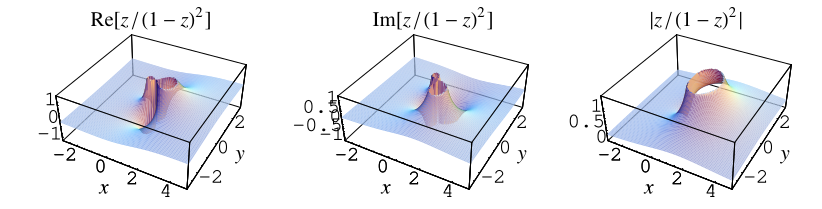
,
|
(3)
|
illustrated above.

The function
|
(1)
|
defined on the unit disk . For
, the Köbe function is a schlicht
function
 |
(2)
|
with
for all
(Krantz 1999, p. 149). For
,
|
(3)
|
illustrated above.
Weisstein, Eric W. "Köbe Function." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/KoebeFunction.html