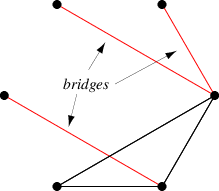
A bridge of a connected graph is a graph edge whose removal disconnects the graph (Chartrand
1985, p. 45; Skiena 1990, p. 177). More generally, a bridge is an edge
of a not-necessarily-connected graph whose removal increases the number of components of
(Harary 1994, p. 26; West 2000, p. 23).
An edge of a connected graph is a bridge iff it does not lie on any cycle. A bridge therefore cannot be a cycle chord.
A bridge is also known as an isthmus, cut-edge (West 2000, p. 23), or cut arc.
Every edge of a tree is a bridge. A connected cubic graph contains a bridge iff it contains an articulation vertex (Skiena 1990, p. 177), i.e., if it is not a biconnected graph.
A graph containing one or more bridges is said to be a bridged graph, while a graph containing no bridges is called a bridgeless graph.
The Wolfram Language function FindEdgeCut[g] returns an edge cut of smallest size for a graph, which corresponds to a graph bridge if the set is of size 1. Precomputed bridges for many named graphs can be listed using GraphData[graph, "Bridges"].
The analog of a graph bridge for vertices is called an articulation vertex.