|
(1)
|
where
is the speed of propagation of a wave in the direction
(i.e.,
,
, and
are the direction cosines)
is known as the wave surface of a given medium (Love 1944, p. 299).
In an isotropic medium, is independent of
,
, and
and is given by
|
(2)
|
where
is the medium density and
and
are the so-called Lamé constants of the solid. The
wave surface is then two-sheeted and both sheets are spheres (Love 1944, p. 299).
In the case of anisotropy, the surface in consists of three sheets corresponding to the values of that are roots of
 |
(3)
|
where the
are functions of
,
, and
in terms of the coefficients of the strain-energy function
(Christoffel 1877, Love 1944, p. 299). Green (1839) showed that the wave surface
for the most general case of an elastic solid that allows the propagation of purely
transverse plane waves consists of a sphere and the two sheets that are the envelope
of the plane (1) subject to the condition
 |
(4)
|
where ,
,
and
are constants characteristic of the surface. The two sheets correspond to what is
known as Fresnel's wave-surface (Love 1944, p. 299).
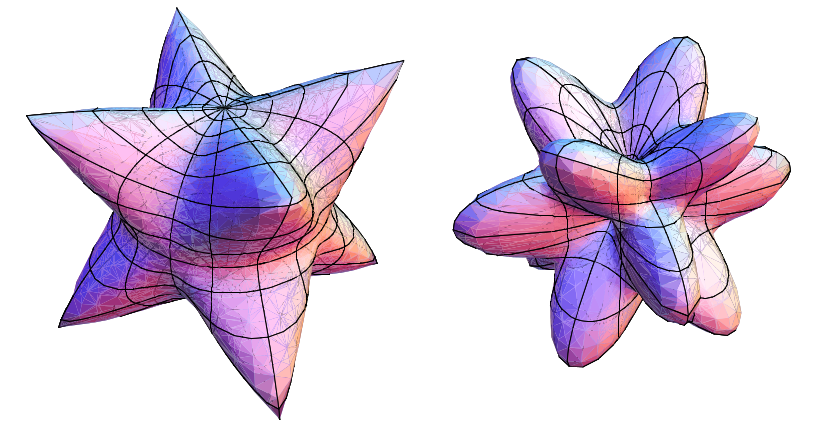
The images above shows the two sheets of Fresnel's wave surface for particular elasticity parameters (JavaView).
von Seggern (1993, p. 304) defines Fresnel's elasticity surface as the quartic surface given by
|
(5)
|
where
|
(6)
|
though this appears to be distinct from the surface described by Love (1944) and on the JavaView website.