There are many mathematical and recreational problems related to folding. Origami, the Japanese art of paper folding, is one well-known example.
It is possible to make a surprising variety of shapes by folding a piece of paper multiple times, making one complete straight cut, then unfolding. For example, a five-pointed star can be produced after four folds (Demaine and Demaine 2004, p. 23), as can a polygonal swan, butterfly, and angelfish (Demaine and Demaine 2004, p. 29). Amazingly, every polygonal shape can be produced this way, as can any disconnected combination of polygonal shapes (Demaine and Demaine 2004, p. 25). Furthermore, algorithms for determining the patterns of folds for a given shape have been devised by Bern et al. (2001) and Demaine et al. (1998, 1999).
Wells (1986, p. 37; Wells 1991) and Gurkewitz and Arnstein (2003, pp. 49-59) illustrate the construction of the equilateral triangle, regular pentagon (illustrated above), hexagon, heptagon, octagon, and decagon using paper folding.
The least number of folds required to create an -gon for
is not known, but some bounds are. In particular, every set of
points is the image of a suitable regular
-gon under at most
folds, where
 |
(1)
|
The first few values are 0, 2, 3, 5, 6, 8, 9, 11, 12, 14, 15, 17, 18, 20, 21, ... (OEIS A007494).
The points accessible from
by a single fold which leaves
,
...,
fixed are exactly those points interior
to or on the boundary of the intersection of the circles
through
with centers at
, for
,
...,
. Given any three points in the plane
,
, and
,
there is an equilateral triangle with polygon vertices
,
,
and
for which
,
,
and
are the images of
,
,
and
under a single fold.
Given any four points in the plane ,
,
, and
, there is some square with polygon
vertices
,
,
, and
for which
,
,
, and
are the images of
,
,
, and
under a sequence of at most three folds. In addition, any four collinear points are
the images of the polygon vertices of a suitable
square under at most two folds. Every five (six) points
are the images of the polygon vertices of suitable
regular pentagon (hexagon)
under at most five (six) folds.
Assuming it were possible to fold paper without restriction, the height of a piece of folded paper would double in thickness each time it was folded. Since one sheet
of typical 20-pound paper has a thickness of about 0.1 millimeter, folding 50 times
(if this were physically possible, which of course it is not) would produce a wad
of height
meters, and folding one more time would make the stack higher than the distance between
the Earth and Sun.
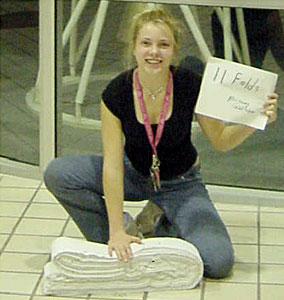
The function
|
(2)
|
gives the loss function for folding paper in half, where is the minimum possible length of the material,
is the thickness, and
is the possible number of folds in a given direction. This
formula indicates how much "normalized" paper has been lost for
folds, and thus sets a limit for the number of times things
of finite thickness can be folded in one direction (Pomona Valley Historical Society).
For
, 1, 2, ... the sequence
gives 0, 1, 4, 14, 50, 186, 714, ... (OEIS A076024).
The formula was derived by high school student Britney Gallivan in December of 2001.
Britney then proceeded to set a new world record by folding first gold foil and then
paper in half a whopping 12 times in January of 2002, thus debunking the assertions
of Math@Home and PBS Kids that paper cannot be folded in half more than eight times.
Britney and her feat were mentioned in the Season 1 episode "Identity
Crisis" (2005) of the television crime drama NUMB3RS.