The elliptic exponential function gives the value of
in the elliptic logarithm
for
and
real such that
.
It is implemented in the Wolfram Language as EllipticExp[u,
a,
b
],
which returns
together with the superfluous parameter
which multiplies the above integral by
a factor of
.
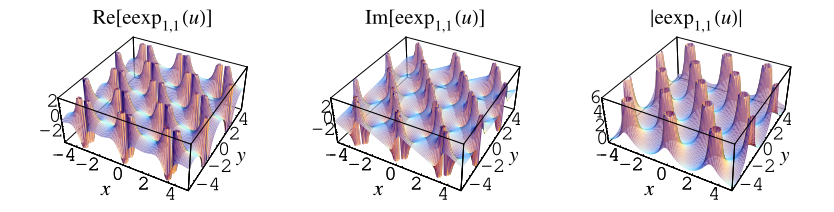
The top plot above shows (red),
(violet), and
(blue) for
. The other plots show
in the complex plane.
The plots above show in the complex plane for
.
As can be seen from the plots, the elliptic exponential function is doubly periodic in the complex plane.