A curve with polar coordinates ,
(1)
studied by the Greek mathematician Nicomedes in about 200 BC, also known as the cochloid. It is the locus of points a fixed distance away from a
line as measured along a line from the focus point (MacTutor
Archive). Nicomedes recognized the three distinct forms seen in this family for circle .)
The conchoid of Nicomedes was a favorite with 17th century mathematicians and could be used to solve the problems of cube duplication ,
angle trisection , heptagon
construction, and other Neusis constructions
(Johnson 1975).
In Cartesian coordinates , the conchoid of
Nicomedes may be written
(2)
or
(3)
The conchoid has area between either branch and
the asymptote is infinite.
A conchoid with
The curvature and tangential
angle are given by
See also Conchoid ,
Conchoid
of de Sluze
Explore with Wolfram|Alpha
References Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Johnson, C. "A Construction for a Regular Heptagon."
Math. Gaz. 59 , 17-21, 1975. Lawrence, J. D. A
Catalog of Special Plane Curves. Loomis,
E. S. "The Conchoid." §2.2 in The
Pythagorean Proposition: Its Demonstrations Analyzed and Classified and Bibliography
of Sources for Data of the Four Kinds of "Proofs," 2nd ed. Loy,
J. "Trisection of an Angle." http://www.jimloy.com/geometry/trisect.htm#curves . MacTutor
History of Mathematics Archive. "Conchoid." http://www-groups.dcs.st-and.ac.uk/~history/Curves/Conchoid.html . Pappas,
T. "Conchoid of Nicomedes." The
Joy of Mathematics. Smith, D. E. History
of Mathematics, Vol. 2: Special Topics of Elementary Mathematics. Steinhaus, H. Mathematical
Snapshots, 3rd ed. Szmulowicz,
F. "Conchoid of Nicomedes from Reflections and Refractions in a Cone."
Amer. J. Phys. 64 , 467-471, Apr. 1996. Wells, D. The
Penguin Dictionary of Curious and Interesting Numbers. Wells, D. The
Penguin Dictionary of Curious and Interesting Geometry. Yates, R. C. "Conchoid." A
Handbook on Curves and Their Properties. Referenced on Wolfram|Alpha Conchoid of Nicomedes
Cite this as:
Weisstein, Eric W. "Conchoid of Nicomedes."
From MathWorld https://mathworld.wolfram.com/ConchoidofNicomedes.html
Subject classifications More... Less...
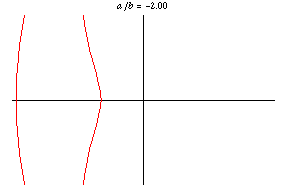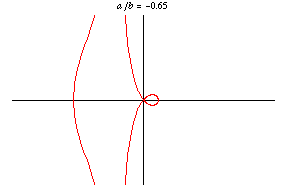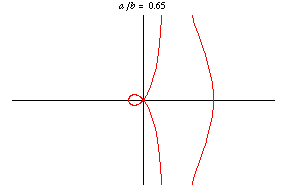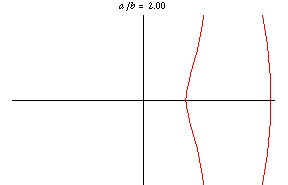
,
, and
. (For
, it obviously degenerates to a circle.)
as an asymptote, and the area between either branch and
the asymptote is infinite.
has a loop for
,
where
,
giving area
