Compact Manifold

A compact manifold is a manifold that is compact as a topological space. Examples are the circle (the only one-dimensional compact manifold) and the -dimensional sphere and torus. Compact manifolds in two dimensions are completely classified by their orientation and the number of holes (genus). It should be noted that the term "compact manifold" often implies "manifold without boundary," which is the sense in which it is used here. When there is need for a separate term, a compact boundaryless manifold is called a closed manifold.

For many problems in topology and geometry, it is convenient to study compact manifolds because of their "nice" behavior. Among the properties making compact manifolds "nice" are the fact that they can be covered by finitely many coordinate charts, and that any continuous real-valued function is bounded on a compact manifold.

For any positive integer , a distinct nonorientable surface can be produced by replacing disks with Möbius strips. In particular, replacing one disk with a Möbius strip produces a cross surface and replacing two disks produces the Klein bottle. The sphere, the -holed tori, and this sequence of nonorientable surfaces form a complete list of compact, boundaryless two-dimensional manifolds.

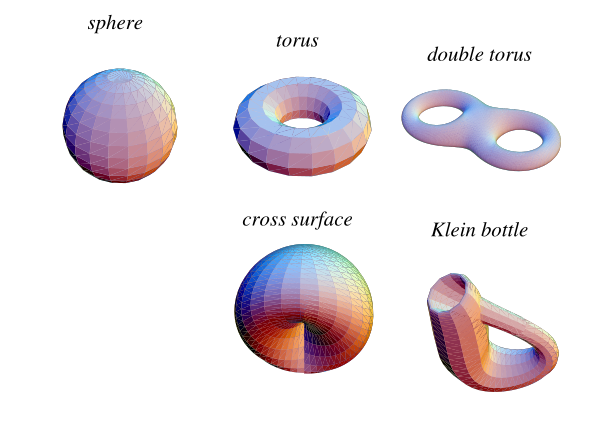
The following table lists the classes of two-dimensional compact manifolds for small , which are also illustrated above.

	0	1	2
orientable	sphere	torus	double torus
nonorientable		cross surface	Klein bottle