A root of a chromatic polynomial is known as a chromatic root (Dong et al. 2005, Alikhani and Ghanbari 2024). Chromatic roots are potentially complex.
Tutte (1970) showed that
cannot be a chromatic root of any chromatic polynomial
where,
is the golden ratio, a result extended to
for positive integer
(Alikhani and Peng 2009).
In contrast,
is a possible chromatic root (Harvey and Royle 2020; e.g., the graphs depicted above),
a result which can be extended to
for integer
(Alikhani and Hasni 2012, Alikhani and Ghanbar 2024)
using the result that if
is a chromatic root, then for any natural number
,
is also a chromatic root.
Sokal (2004) showed that chromatic roots are dense in the complex plane (Cameron and Morgan 2016).
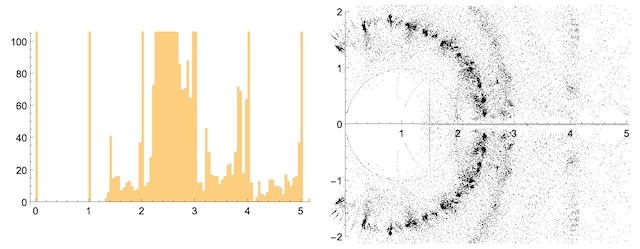
An interval in which no chromatic roots are possible is known as a chromatic root-free interval. The plots above show a histogram of chromatic roots along the real axis and the positions of chromatic roots in the complex plane for graphs in GraphData (the latter of which shows clear deviations from uniformity).