An algebraic surface with affine equation
(1)
where Chebyshev polynomial of the
first kind and
(2)
where the matrices have dimensions ordinary
double points as singularities. The first few surfaces are given by
The
(6)
singular points (Chmutov 1992), giving the sequence 0, 1, 3, 14, 28, 57, 93, 154, 216, 321, 425, 576, 732, 949, 1155, ... (OEIS A057870 )
for
Based on Chmutov's equations, Banchoff (1991) defined the simpler set of surfaces
(7)
where even and Chebyshev
polynomial of the first kind . For example, the surfaces illustrated above have
orders 2, 4, and 6 and are given by the equations
See also Goursat's Surface ,
Ordinary
Double Point ,
Superellipse ,
Tanglecube
Explore with Wolfram|Alpha
References Banchoff, T. F. "Computer Graphics Tools for Rendering Algebraic Surfaces and for Geometry of Order." In Geometric
Analysis and Computer Graphics: Proceedings of a Workshop Held May 23-25, 1988 Chmutov, S. V. "Examples of Projective
Surfaces with Many Singularities." J. Algebraic Geom. 1 , 191-196,
1992. Hirzebruch, F. "Singularities of Algebraic Surfaces and Characteristic
Numbers." In The
Lefschetz Centennial Conference, Part I: Proceedings of the Conference on Algebraic
Geometry, Algebraic Topology, and Differential Equations, Held in Mexico City, December
10-14, 1984 Sloane, N. J. A. Sequence A057870
in "The On-Line Encyclopedia of Integer Sequences." Trott,
M. Graphica
1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael
Trott. Trott,
M. The
Mathematica GuideBook for Graphics. http://www.mathematicaguidebooks.org/ . Referenced
on Wolfram|Alpha Chmutov Surface
Cite this as:
Weisstein, Eric W. "Chmutov Surface."
From MathWorld https://mathworld.wolfram.com/ChmutovSurface.html
Subject classifications
is a Chebyshev polynomial of the
first kind and
is a polynomial defined by

. These represent surfaces in
with only ordinary
double points as singularities. The first few surfaces are given by
th
order such surface has

,
2, .... For a number of orders
, Chmutov surfaces have more ordinary double points than any
other known equations of the same degree.

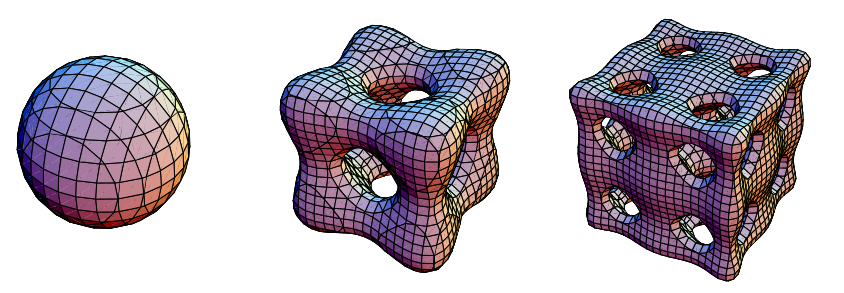
is even and
is again a Chebyshev
polynomial of the first kind. For example, the surfaces illustrated above have
orders 2, 4, and 6 and are given by the equations