TOPICS
Search

Ber

DOWNLOAD Mathematica NotebookDownload Wolfram Notebook
Ber5

The function ber_nu(z) is defined through the equation

J_nu(ze^(3pii/4))=ber_nu(z)+ibei_nu(z),
(1)

where J_nu(z) is a Bessel function of the first kind, so

ber_nu(z)=R[J_nu(ze^(3pii/4))],
(2)

where R[z] is the real part.

The function is implemented in the Wolfram Language as KelvinBer[nu, z].

The function ber_nu(z) has the series expansion

ber_nu(z)=(1/2z)^nusum_(k=0)^infty(cos[(3/4nu+1/2k)pi])/(k!Gamma(nu+k+1))(1/4z^2)^k,
(3)

where Gamma(z) is the gamma function (Abramowitz and Stegun 1972, p. 379), which can be written in closed form as

ber_nu(z)=1/2e^(-3ipinu/4)z^nu[(-1)^(1/4)z]^(-nu) ×[e^(3piinu/2)I_nu((-1)^(1/4)z)+J_nu((-1)^(1/4)z)],
(4)

where I_nu(z) is a modified Bessel function of the first kind.

Ber
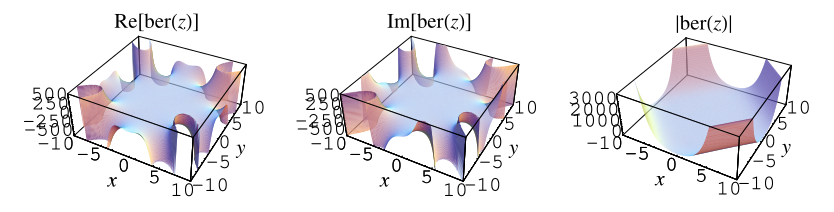
BerReIm
BerContours

The special case nu=0, commonly denoted ber(x), corresponds to

J_0(isqrt(i)z)=ber(z)+ibei(z),
(5)

where J_0(z) is the zeroth order Bessel function of the first kind. The function ber_0(z)=ber(z) has the series expansion

ber(z)=1+sum_(n=1)^infty((-1)^n(1/2z)^(4n))/([(2n)!]^2)
(6)

which can be written in closed form as

ber(z)=1/2[I_0((-1)^(1/4)z)+J_0((-1)^(1/4)z)]
(7)
=1/2[I_0((-1)^(1/4)z)+I_0((-1)^(3/4)z)].
(8)

See also

Bei, Bessel Function, Kei, Kelvin Functions, Ker

Explore with Wolfram|Alpha

References

Abramowitz, M. and Stegun, I. A. (Eds.). "Kelvin Functions." §9.9 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 379-381, 1972.Prudnikov, A. P.; Marichev, O. I.; and Brychkov, Yu. A. "The Kelvin Functions ber_nu(x), beinu(x), ker_nu(x) and kei_nu(x)." §1.7 in Integrals and Series, Vol. 3: More Special Functions. Newark, NJ: Gordon and Breach, pp. 29-30, 1990.Spanier, J. and Oldham, K. B. "The Kelvin Functions." Ch. 55 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 543-554, 1987.

Referenced on Wolfram|Alpha

Ber

Cite this as:

Weisstein, Eric W. "Ber." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Ber.html

Subject classifications