Bean Curve

There are a few plane curves known as "bean curves."

The bean curve identified by Cundy and Rowllet (1989, p. 72) is the quartic curve given by the implicit equation

It has horizontal tangents at and vertical tangents at and . The area enclosed by the curve is given by

(OEIS A193505). The geometric centroid of the interior by

and the area moment of inertia tensor of the interior by

(E. Weisstein, Feb. 3-5, 2018). The perimeter is given by

(OEIS A193506).

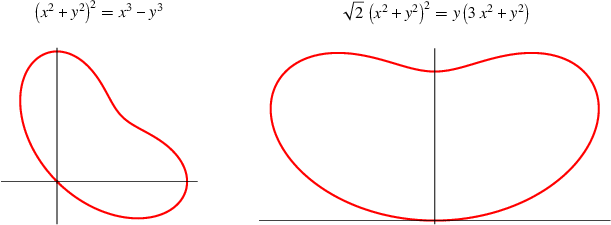
A second bean curve that more closely resembles an actual bean (in particular, a lima bean), here called the "lima bean curve," is given by the simple polar equation

(Wassenaar; left figure above). It also is a quartic curve and has Cartesian equation

If the lima bean is rotated so that it appears entirely in the half-plane and is oriented symmetrically about the -axis (right figure above), its Cartesian equation becomes

The parametric equations of the original polar curve are

This curve has maximum values and minimum values , where is the real root of . The area enclosed by the curve is

(cf. OEIS A244978). The geometric centroid of the interior is given by

and the perimeter by

(OEIS A336501). The area moment of inertia tensor of the interior is given by