The Barth sextic is a sextic surface in complex three-dimensional projective space having the maximum possible number of ordinary double points, namely 65. The surface was discovered by W. Barth in 1994, and is given by the implicit equation
 |
where
is the golden ratio.
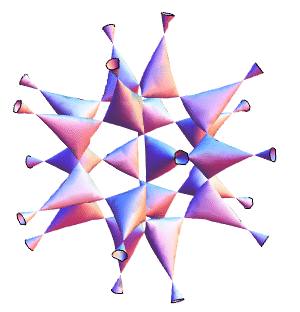
Taking
gives the surface in 3-space illustrated above, which retains 50 ordinary
double points.
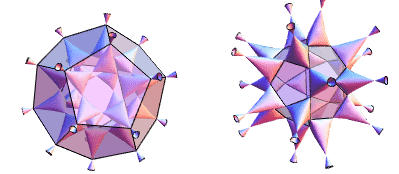
Of these, 20 nodes are at the vertices of a regular dodecahedron of side length and circumradius
(left figure above), and 30 are at the vertices of a
concentric icosidodecahedron and circumradius
1 (right figure).
The Barth sextic is invariant under the icosahedral group. Under the map
the surface is the eightfold cover of the Cayley cubic (Endraß 2003).

The Barth sextic appeared on the cover of the March 1999 issue of Notices of the American Mathematical Society (Dominici 1999).