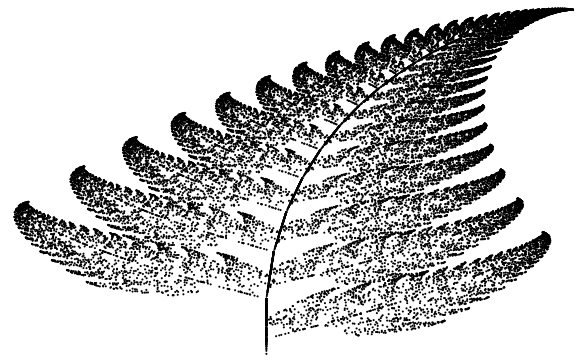
The attractor of the iterated
function system given by the set of "fern functions"
(Barnsley 1993, p. 86; Wagon 1991). These affine transformations are contractions. The tip of the fern (which resembles the black
spleenwort variety of fern) is the fixed point of
See also Barnsley's Tree ,
Dynamical System ,
Fractal ,
Iterated
Function System
Explore with Wolfram|Alpha
References Barnsley, M. Fractals Everywhere, 2nd ed. Gleick, J. Chaos:
Making a New Science. Trott,
M. Graphica
1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael
Trott. Wagon,
S. "Biasing the Chaos Game: Barnsley's Fern." §5.3 in Mathematica
in Action. Referenced
on Wolfram|Alpha Barnsley's Fern
Cite this as:
Weisstein, Eric W. "Barnsley's Fern."
From MathWorld https://mathworld.wolfram.com/BarnsleysFern.html
Subject classifications
![[0.85 0.04; -0.04 0.85][x; y]+[0.00; 1.60]](/images/equations/BarnsleysFern/Inline3.svg)
![[-0.15 0.28; 0.26 0.24][x; y]+[0.00; 0.44]](/images/equations/BarnsleysFern/Inline6.svg)
![[0.20 -0.26; 0.23 0.22][x; y]+[0.00; 1.60]](/images/equations/BarnsleysFern/Inline9.svg)
![[0.00 0.00; 0.00 0.16][x; y]](/images/equations/BarnsleysFern/Inline12.svg)
, and the tips of the lowest two branches are the images
of the main tip under
and
(Wagon 1991).