An additive cellular automaton is a cellular automaton whose rule is compatible with an addition of states. Typically, this addition is derived from modular arithmetic. Additive rules allow the evolution for different initial conditions to be computed independently, then the results combined by simply adding. The results for arbitrary starting conditions can therefore be computed very efficiently by convolving the evolution of a single cell with an appropriate convolution kernel (which, in the case of two-color automata, would correspond to the set of initially "active" cells).
A simple example of an additive cellular automaton is provided by the rule 90 elementary cellular automaton.
As can be seen from the graphical representation of this rule, the rule as a function
of left, central, and right neighbors is simply given by the sum of the rules for
the left and right neighbors taken modulo 2, where white cells are assigned the value
0 and black cells are assigned 1. (This is equivalent to the XOR
operation and means that "adding" two white cells or two black cells gives
a white cell, while adding one white and one black cells gives a black cell.) For
example, the rule for (1, 1, 1) is , the rule for (1, 1, 0) is
, the rule for (1, 0, 1) is
, and so on. Repeating this for each of the
possible states of neighbors gives
|
(1)
|
which is exactly the binary string defining the behavior of rule 90 (this rule is assigned the number 90 is because in binary).

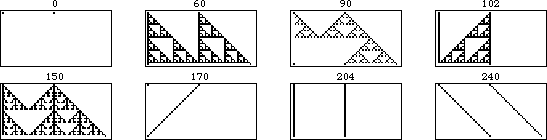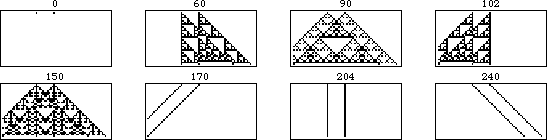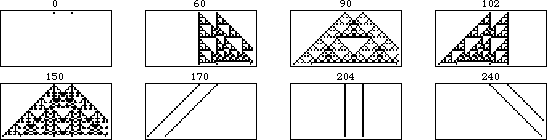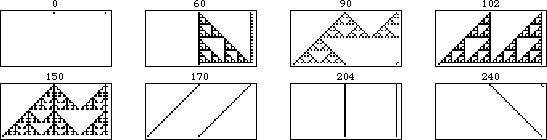
The evolution of shifted versions of rule 90 are illustrated in the above figure. The figure on the left shows 31 iterations of rule
90 for an initial condition consisting of a single black square. Moving to the
right, each figure shows the results of adding an additional black cell with displacement
to the starting condition, increasing one generation per frame.

The illustration above shows the additivity more explicitly. In this animation, each frame corresponds to an initial conditions with the right cell shifted one unit further to the right. As can be seen, the portion of the pattern that does not overlap remains unchanged, while the overlapping portion is additive under the XOR operation.
In general, a cellular automaton with colors is additive if its rules can be written as a sum of
integer multiples of its neighbors (mod
), where the integers can range from 0 to
. There are therefore
additive rules among the
possible rules with
colors and range
(Wolfram 2002, p. 952).
The table below summarize the eight additive rules for the elementary
cellular automata (
and
gives
). In the table,
denotes the neighbor located at position
relative to the center.
For additivity of the above automata, the properties required were associativity and commutativity. It is possible to generalize the notion of additivity to other
types of addition. In general, let denote the cellular automaton evolution history of
,
and let
denote a binary operator acting on the values
of cells and, by extension, to their states and evolution. Then
is an additive cellular automaton with respect to
if
|
(2)
|
Some cellular automata have no interesting , but others do, and these additions can be used
to speed up calculations.
Rule 250 provides another example of an additive elementary cellular automaton under the operation OR(). By examining the set of rules, it can be verified
that in each case, the resultant state is black if either (or both) neighbors is
black, and white only if both neighbors are white. This corresponds to the set of
rules
|
(3)
|
which is identical to the definition of rule 250.


Generation-by-generation differences for the first few shifts and the entire pattern as a function of shift are illustrated above.
As a result of additivity, the evolutions of additive cellular automata behave similarly to the solutions of linear partial differential equations. In particular, they admit analogs of Green's functions such that, given an initial condition, the resulting evolution can be found by convolving the evolution of a single cell (which can be viewed as the analog of an integral kernel) with the initial condition (Wolfram 2002, p. 952).