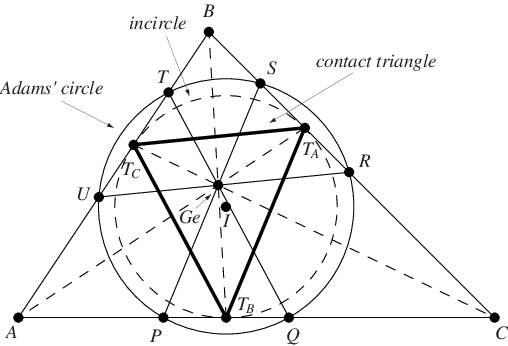
Given a triangle , construct the contact
triangle
.
Now extend lines parallel to the sides of the contact
triangle from the Gergonne point. These intersect the triangle
in the six points
,
,
,
,
,
and
. C. Adams proved in 1843 that these
points are concyclic in a circle
now known as the Adams' circle.
Adams' circle is a central circle with circle function
 |
(1)
|
which does not correspond to any notable triangle center. Its radius is the complicated expression
 |
(2)
|
where
is the inradius and
is the semiperimeter of
the reference triangle and
|
(3)
|
The center of Adams' circle is the incenter of (Honsberger 1995, pp. 62-74).
No notable triangle centers lie on Adams' circle.
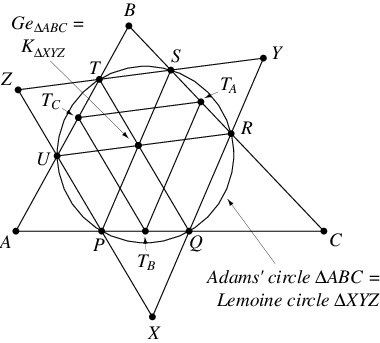
Extend the segments ,
, and
to form a triangle
. Then the Gergonne point
of
is the symmedian
point of
,
and Adams' circle of
is the first Lemoine circle of
(Honsberger 1995, p. 98).