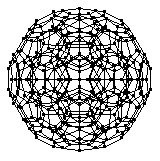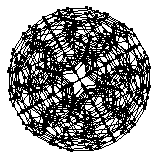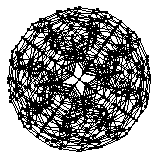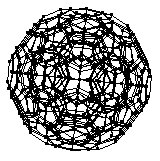
The 120-cell is a finite regular four-dimensional polytope with Schläfli symbol . It is also known as the hyperdodecahedron or hecatonicosachoron,
and is composed of 120 dodecahedra, with 3 to an
edge, and 720 pentagons (Coxeter 1973, p. 264).
The 120-cell has 600 vertices (Coxeter 1969) and 1200 edges. It is one of the six
regular polychora.
In the plate following p. 176, Coxeter (1973) illustrates the polytope.
The dual of the 120-cell is the 600-cell.
The vertices of the 120-cell with circumradius and edge length
are given by the following sets, where
is the golden ratio (Coxeter
1969, p. 404).
1. A set of 24 vectors given by and all its permutations.
2. A set of 64 given by
and all its permutations.
3. A set of 64 given by
and all its permutations.
4. A set of 64 given by
and all its permutations.
5. A set of 96 given by
and all its even permutations.
6. A set of 96 given by
and all its even permutations.
7. A set of 192 given by
and all its even permutations.
There are 30 distinct nonzero distances between vertices of the 120-cell in 4-space.


The top image above shows a projection of the 120-cell laser-etched into glass, and the two bottom images show a projection visualized as a metal sculpture. Both works were created by digital sculptor Bathsheba Grossman (http://www.bathsheba.com/).
The skeleton of the 120-cell, shown above in several projections, is a 4-regular graph (i.e., a quartic graph of girth 5 (pentagonal
cycles) and diameter 15. The numbers of vertices at graph distance , 1, 2, ... from a given vertex on the skeleton of the 120-cell
are 1, 4, 12, 24, 36, 52, 68, 76, 78, 72, 64, 56, 40, 12, 4, and 1 (OEIS A108997).
The 120-cell has graph spectrum
![4^1(alpha,beta,gamma)^(25)(mu,eta,sigma)^(36)[1/2(3+/-sqrt(13))]^(16)[1/2(-1+/-sqrt(21))]^(16)(-1+/-sqrt(2))^(48)[1/2(5+/-sqrt(5))]^91^(40)0^(18)(-1)^8(-2)^8(-3phi+2)^4(3phi-1)^4(+/-sqrt(5))^(24)phi^(24)(1-phi)^(24)(phi-2)^(24)(-1-phi)^(30),](/images/equations/120-Cell/NumberedEquation1.svg) |
where ,
, and
are the real roots of
,
,
,
and
are the roots of
, and
is the golden
ratio. The skeleton of the 120-cell is implemented in the Wolfram
Language as GraphData["HundredTwentyCellGraph"].
The independence number of the 120-cell skeleton is 220 (Debroni et al. 2010) and its chromatic number is 3 (S. Wagon and R. Pratt, pers. comm., Dec. 2, 2011). R. Pratt has also found a balanced 3-coloring having 200 vertices of each color.
The 120-cell has
 |
distinct nets (Buekenhout and Parker 1998). The order of its automorphism group is (Buekenhout and Parker 1998).